Funktionen und Schaubilder
In einer der Pflichtteil-Aufgaben, meistens in Aufgabe 5 wird der Zusammenhang
zwischen Schaubildern und Funktionsgraphen geprüft.
- Manchmal sollen bestimmte Eigenschaften nachgewiesen werden.
- Manchmal wird der Zusammenhang zwischen Ableitung und Originalfunktion oder zwischen Original- und Stammfunktion abgefragt.
- Hin und wieder soll man Funktionsterme den jeweils passenden Schaubildern zuordnen (und die Zuordnung natürlich auch begründen).
Hochpunkte
Ein Hochpunkt ist dadurch gekennzeichnet, dass die Ableitungsfunktion ihr Vorzeichen von + nach - wechselt. Die Steigung nimmt anfangs stark zu, wird immer flacher, ist Null im Hochpunkt, kehrt sich um und fällt dann immer mehr ab.
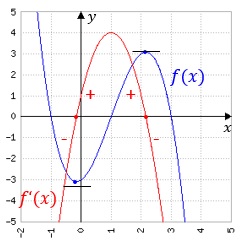
Ein Tiefpunkt ist dadurch gekennzeichnet, dass die Ableitungsfunktion ihr Vorzeichen von – nach + wechselt. Die Steigung fällt anfangs stark ab, wird immer flacher, ist Null im Tiefpunkt, kehrt sich um und wird dann immer steiler.
Wendepunkte und Sattelpunkte
Wendepunkte liegen immer an den Extremstellen (Hoch- und Tief-punkten) der Ableitung vor (Kriterium f''(x)=0). Wenn gleichzeitig auch f'(x)=0 gilt, spricht man von einem Sattelpunkt. Dies ist eine besondere Form eines Wendepunkts.
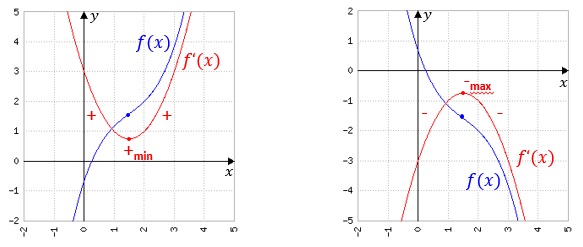
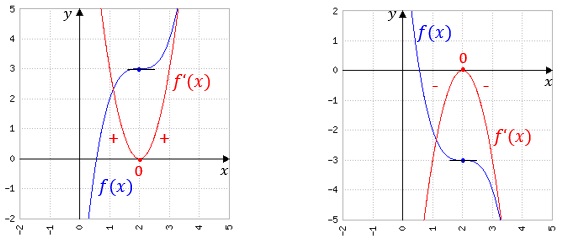
Untersuchung auf Monotonie
Mit der ersten Ableitung f'(x) lässt sich auch feststellen, ob eine Funktion f(x) in einem Intervall [a;b] (streng) monoton wächst oder (streng) monoton fällt. Grund: f'(x) gibt die Steigung der Tangente an der Stelle x an.
- f'(x)>0 ⇒ f ist streng monoton wachsend
- f'(x)=0 ⇒ f ist monoton wachsend
- f'(x)<0 ⇒ f ist streng monoton fallend
- f'(x)=0 ⇒ f ist monoton fallend
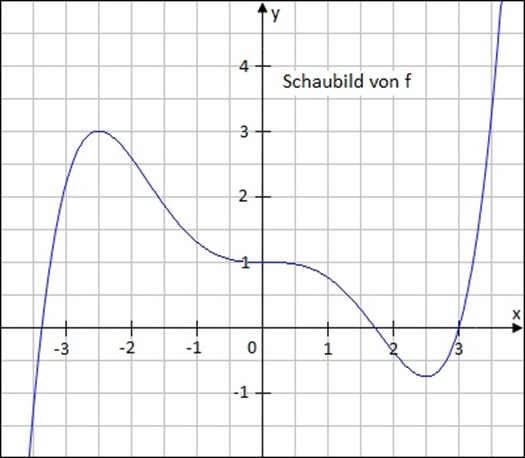
In den Abi-Aufgaben findet man Formulierungen wie "zeigen Sie, dass die Funktion f im Intervall [a;b] stets zunimmt", bzw. analog, "stets abnimmt". Nun wissen Sie, dass Sie in einem solchen Fall f'(x)>0 bzw. f'(x)<0 im betrachteten Intervall (oder auch für die gesamte Funktion) nachweisen müssen.
| Downloads |
PowerPoint